Snowshoe hare example analyses
Jessica Melbourne-Thomas, Ben Raymond, Andrew Constable, Simon Wotherspoon
2013
The QPress package provides facilities for qualitatively modelling the impact of a press perturbation upon a network model. This document illustrates the basic features of the package through a simple example.
Introduction
The QPress package provides facilities for qualitatively modelling the impact of a press perturbation upon a network model in the style of Melbourne-Thomas et al. (2012).
In this document we illustrate some of the basic facilities provided by the package using the Snowshoe hare example from Dambacher and Ramos-Jiliberto (2007).
Dambacher and Ramos-Jiliberto (2007) describes five alternative models for the interactions between the snowshoe hare, its major predator and the supporting vegetation. These five models are reproduced in Table 1, and show the interactions of the hare \(H\) with the vegetation \(V\) and predator \(P\).
| Model A | |
| Model B | |
| Model C | |
| Model D | |
| Model E |
Table 1: Alternate models for the snowshoe hare system.
Model Definition
The first step of any analysis is to define an appropriate model structure.
A directed graph representation of a model may be constructed from simple textual description with the parse.digraph and read.digraph functions. The parse.digraph allows the edges of the graph to be specified as a vector of character strings.
library(QPress)
## Read a textual model description
modelA <- parse.digraph(c("V-*V", "P-*P", "V*->H", "H*->P"))Alternately, the edge descriptions can be stored in a text file, one edge per line, and read and written with read.digraph and write.digraph respectively
## Write/read a model description to a text file
write.digraph(modelA,"modelA.txt")
modelA <- read.digraph("modelA.txt")Within R, the graph is represented as an edge list, a dataframe of directed edges.
modelA
#> From To Group Type Pair
#> 1 V V 0 N 1
#> 2 P P 0 N 2
#> 3 V H 0 P 3
#> 4 H P 0 P 4
#> 7 H V 0 N 3
#> 8 P H 0 N 4This dataframe records the nodes connected by the directed edge (To and From), whether the edge represents a positive (P) or negative (N) impact (Type), and which edges were paired in the original specification (Pair). As will be demonstrated below, it also it is possible to group edges (Group). For example, the edge connecting \(V\) and \(H\) in model A has been separated into the positive impact of \(V\) upon \(H\), and the negative impact of \(H\) upon \(V\).
Models B to E may be defined similarly:
modelB <- parse.digraph(c("V-*V", "P-*P", "V*->H", "H*->P", "V->P"))
modelC <- parse.digraph(c("V-*V", "H-*H", "P-*P", "V*->H", "H*->P", "V->P"))
modelD <- parse.digraph(c("V-*V", "P-*P", "V*->H", "H*->P", "V*->P"))
modelE <- parse.digraph(c("V-*V", "H-*H", "P-*P", "V*->H", "H*->P", "V*->P"))It is also possible to combine these four models into one “super” model using the mechanism of uncertain edges. Edges are allocated into groups according to the number of dashes in their text definition or the line style in their Dia definition. The (directed) edges common to the four models are specified as one group, and the disjoint edges as a second.
## Model with uncertain edges
modelBCDE <- parse.digraph(c("V-*V", "P-*P", "V*->H", "H*->P", "V->P", "H--*H", "V*--P"))
modelBCDE
#> From To Group Type Pair
#> 1 V V 0 N 1
#> 2 P P 0 N 2
#> 3 V H 0 P 3
#> 4 H P 0 P 4
#> 5 V P 0 P 5
#> 6 H H 1 N 6
#> 10 H V 0 N 3
#> 11 P H 0 N 4
#> 14 P V 1 N 7When simulating from this super model, edges from the first group (group 0) can be treated as “required” and then will be included in all simulations, while second group (group 1) can be treated as “uncertain”, and included or excluded at random.
Many models will not be stable unless the majority of nodes are self limiting. The enforce.limitations function adds a self limiting edge to every node. So models C and E could be obtained from models B and D as:
## Add self-limitation to all nodes
modelC <- enforce.limitation(modelB)
modelE <- enforce.limitation(modelD)The adjacency matrix can be constructed from the edge list with the adjacency.matrix function:
adjacency.matrix(modelA, labels = TRUE)
#> H P V
#> H 0 -1 1
#> P 1 -1 0
#> V -1 0 -1High Level Simulation
Many analyses can be performed with the high level simulation function system.simulate. This function simulates random community matrices that:
- are consistent with the given signed directed graph,
- correspond to a system with a stable equilibrium, and optionally
- are consistent with a set of validation criteria,
and returns the negative inverses and the non-zero elements of the simulated community matrices. The properties of these simulated matrices can be interactively explored with the impact.barplot and weight.density functions.
Dambacher and Ramos-Jiliberto (2007) note that model A predicts that a positive press perturbation of the vegetation always results in an increase in hare numbers, yet manipulation experiments have shown that this is not always the case, suggesting that model A is not an adequate description of the physical system.
To show that model A predicts an increase in hare numbers following a positive press perturbation of the vegetation, we simulate 1000 community matrices corresponding to model A:
simA <- system.simulate(1000, modelA)and explore the simulations with impact.barplot:
impact.barplot(simA)This creates an interactive control panel that allows the user to specify a press perturbation and optionally a validation criterion, and then displays the impact of the perturbation on each node as a barplot. This plot shows the fraction of positive (orange), zero (brown), and negative (blue) outcomes at each node. Selecting a positive (+) perturbation of the \(V\) node in the perturbation panel, and pressing the update button produces the first barplot shown in Figure 1. This plot shows that a positive press perturbation to the vegetation always has a positive impact at each node.
Repeating this process for model B
simB <- system.simulate(1000, modelB)
impact.barplot(simB)produces the second barplot in in Figure 1. This shows that for model B, almost 40% of the community matrices simulated yield a decrease in hare numbers following a positive press perturbation to the vegetation.
The impact.barplot function takes a second argument epsilon that controls sensitivity to change — outcomes smaller than epsilon are treated as zero. The third barplot in in Figure 1 shows the result of simulating from the combined model BCDE and applying a positive press perturbation to V, but treating changes to the equilibrium value of less than 5% as neglible.
simBCDE <- system.simulate(1000, modelBCDE)
impact.barplot(simBCDE, epsilon = 0.05)We can limit the plot to just those cases in which hares decrease in response to the perturbation applied to \(V\) by selecting a negative (-) for the \(H\) node in the monitor panel. This yields the fourth barplot in in Figure 1.

Figure 1 Model outcomes in response to a positive press perturbation to the vegetation. Each plot shows the fraction of positive (orange), zero (brown), and negative (blue) outcomes at each node following a positive press perturbation to the vegetation.
The weight.density function can be used to explore the magnitude of the edge weights (model interaction strengths) associated with a particular outcomes. For example, the call
weight.density(simBCDE)produces an interactive control panel that allows the user to specify a press perturbation, an observed outcome, and a subset of edges. For ease of identification, the edge selection panel is laid out in the same structure as the adjacency matrix.
adjacency.matrix(modelBCDE, required.groups = 0:1)
#> [,1] [,2] [,3]
#> [1,] -1 -1 1
#> [2,] 1 -1 1
#> [3,] -1 -1 -1The community matrices simulated from the model are classified as either consistent or inconsistent with the observed outcome given the specified press perturbation, and for each selected edge, density plots of the edge weights are produced for the two groups of matrices. For matrices consistent with the observed outcome, the density of edge weights is shown in blue, while for those inconsistent with the observed outcome, the density of edge weights is shown in red. For readability, the plots are labelled by the indices that edge would have in the adjacency matrix.
For the simulated matrices from model BCDE, selecting a positive (+) perturbation of the \(V\) node in the perturbation panel, and negative (-) outcome for \(H\) in the monitor panel and selecting all edges produces the suite of density plots shown in Figure 2. Each plot in the figure corresponds to an edge of model BCDE, and the blue lines show the density of the edge weights where hares decreased, while the red lines show the density of edge weights where hares increased. So for example, the plot labelled 2:2 corresponds to the self limiting edge on \(P\), and shows that decreases in hare numbers following a positive press perturbation to vegetation is associated with stronger self limitation of the predator.
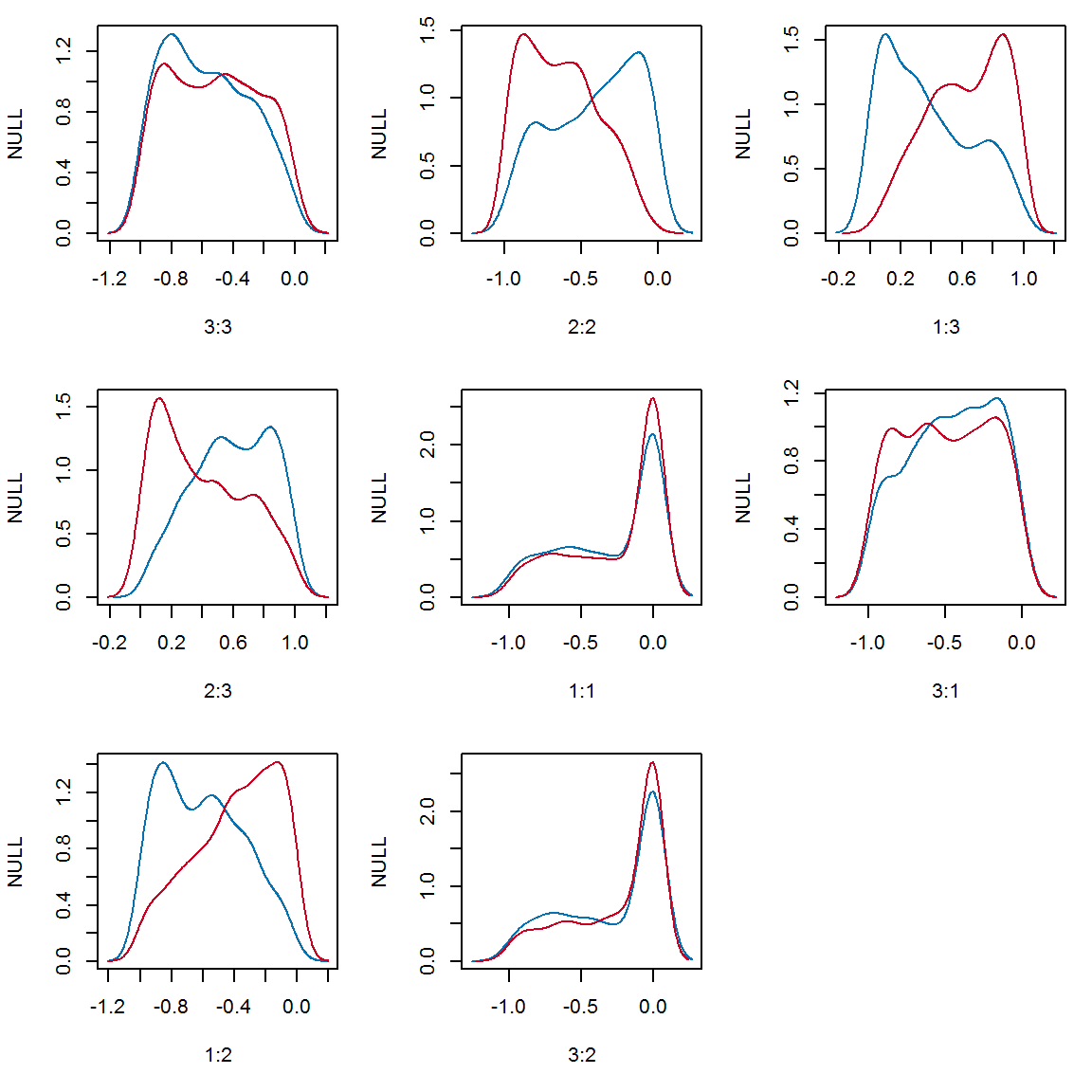
Figure 2: Edge weight density plots for a decrease in hares following a positive press perturbation to vegetation in model BCDE. Each plot corresponds to an edge, and shows the distribution of edge weights when hares decrease (blue) and when hares increase (red).
More complex validation criteria can be specified by passing validation functions generated by press.validate to system.simulate directly. For example, the call:
## Simulate 1000 community matrices from the uncertain model, st
## 1. A positive perturbation of P leads to a reduction in H
## 2. A positive perturbation of V leads to an increase in V
simBCDE1 <- system.simulate(1000, modelBCDE,
validators = list(
press.validate(modelBCDE,
perturb = c(P = 1),
monitor = c(H = -1)),
press.validate(modelBCDE,
perturb = c(V = 1),
monitor = c(V = 1))))simulates community matrices consistent with model BCDE that satisfy the validation criteria that hares decrease following a positive press perturbation of the predators, and vegetation increases following a press perturbation of vegetation. As system.simulate attempts to generate a fixed number of matrices, the simulation may fail to terminate of too stringent a validation criteria is set.
Competing models can be compared based on the frequency with which the models reproduce an observed outcome. At a simple level, the more frequently a model reproduces a observed outcome, the more likely the model is correct. This notion can be embedded within Bayesian framework to produce a formal system of model comparison. Suppose a positive press perturbation of vegetation is observed to produce a decrease in hare numbers. It is believed that the system can be described by model B, C, D, or E, but it is believed that models D and E are slightly more plausible than models B and C. Models B and C are both assigned prior probabilities of \(4/16\) and models D and E are assigned prior probabilities of \(5/16\) each.
prior <- c(B=3/16,C=3/16,D=5/16,E=5/16)The marginal likelihood of each model is the fraction of simulate community matrices that yield an prediction consistent with the observed impact:
## Compute the likelihood for each model
simB <- system.simulate(1000, modelB,
validators=list(
press.validate(modelB, perturb = c(V = 1),
monitor = c(H = -1))))
simC <- system.simulate(1000, modelC,
validators=list(
press.validate(modelC, perturb = c(V = 1),
monitor = c(H = -1))))
simD <- system.simulate(1000, modelD,
validators=list(
press.validate(modelD, perturb = c(V = 1),
monitor = c(H = -1))))
simE <- system.simulate(1000, modelE,
validators=list(
press.validate(modelE, perturb = c(V = 1),
monitor = c(H = -1))))
likelihood <- c(B = simB$accepted / simB$total,
C = simC$accepted / simC$total,
D = simD$accepted / simD$total,
E = simE$accepted / simE$total)The posterior probabilities for the four models are then
posterior <- prior * likelihood / sum(prior*likelihood)
posterior
#> B C D E
#> 0.1482024 0.1881286 0.2792648 0.3844042suggesting that model E is the most likely model.
Low Level Simulation
The system.simulate function is a wrapper for the lower level functions community.sampler, stable.community, press.validate and press.impact. More flexible simulations can be constructed in terms of these primitives.
The community.sampler function constructs functions for sampling community matrices from a given model
s <- community.sampler(modelBCDE)This returns a list with components select, community, weights, weight.labels and uncertain.labels. The select component randomly selects which uncertain edges will be included or excluded from the model in subsequent simulations. This is a function takes as single argument the probability with which any uncertain edge is to be retained in the model:
## Select uncertain edges
s$select(p=0.5)This function returns a vector that indicates which uncertain edges have been retained. The community component generates a random community matrix consistent with the model and the selected of uncertain edges:
W <- s$community()
W
#> [,1] [,2] [,3]
#> [1,] -0.4545210 -0.6312181 0.4460041
#> [2,] 0.2200059 -0.8027115 0.2359806
#> [3,] -0.3911064 0.0000000 -0.5199113The non-zero elements of this matrix can be extracted with the weights element:
s$weights(W)
#> [1] -0.5199113 -0.8027115 0.4460041 0.2200059 0.2359806 -0.4545210
#> [7] -0.3911064 -0.6312181 0.0000000and the corresponding edge labels, and the labels of the uncertain edges are given by weight.labels and uncertain.labels:
s$weight.labels
#> [1] "V -* V" "P -* P" "V -> H" "H -> P" "V -> P" "H -* H" "H -* V" "P -* H"
#> [9] "P -* V"
s$uncertain.labels
#> [1] "H -* H" "P -* V"The stable.community function determines whether community matrix corresponds to a system with a stable equilibrium:
stable.community(W)
#> [1] TRUEThe press.impact function constructs a function to compute the impact of a system to a given press perturbation:
## Evaluate impact of a perturbation to V
impact <- press.impact(modelBCDE, perturb = c(V = 1))
impact(W)
#> [1] 0.6083370 0.5976411 1.4657799
signum(impact(W))
#> [1] 1 1 1The press.validate function constructs a function to determine whether a community matrix satisfies a given validation criterion:
## a positive perturbation to V should produce a reduction in H
g <- press.validate(modelBCDE,perturb=c(V=1),monitor=c(H=-1))
g(W)
#> [1] FALSEReferences
Dambacher, Jeffrey M, and Rodrigo Ramos-Jiliberto. 2007. “Understanding and Predicting Effects of Modified Interactions Through a Qualitative Analysis of Community Structure.” The Quarterly Review of Biology 82 (3). JSTOR: 227–50.
Melbourne-Thomas, J, S Wotherspoon, B Raymond, and A Constable. 2012. “Comprehensive Evaluation of Model Uncertainty in Qualitative Network Analyses.” Ecological Monographs 82 (4). Eco Soc America: 505–19.